Visualizing The Beauty Of Vibrato
11:54 minutes

What makes Pablo Casals’ playing so wonderful? Why does sound produced on an erhu—a two-stringed chinese fiddle—differ from a cello? As a musician, Elaine Chew wanted to unlock the secrets of the musical vibration known as vibrato. As a mathematician, she used the tools of science to do it. In a recent study in the Journal of Mathematics and Music, Chew and her team analysed the frequency of vibrato among a number of different instruments using a technique developed in quantum physics to visualize molecular vibrations. Chew and her co-author, Khalid Rajab, an assistant professor of electrical engineering at Queen Mary University of London, join Ira to discuss how mathematics can explain the beauty of vibrato.
Elaine Chew is a professor of Digital Media in the Center for Digital Music at the Queen Mary University of London in London, England.
Khalid Rajab is an assistant professor of Electronic Engineering at Queen Mary University of London in London, England.
IRA FLATOW: This is “Science Friday.” I’m Ira Flatow. Pablo Casals, that’s him playing his cello. He’s one of the great musicians of the 20th century, and best remembered, perhaps, for his recordings of the Bach cello suites. Now what stands out in particular is his mastery of the controlled vibrato, a movement of the finger on the string. And it’s said to sweeten the note.
[CELLO PLAYING]
Now the way Casals plays vibrato is unique, and beautiful, and different from other equally talented musicians. But how is it? When you listen, you can’t quite put your finger on that difference. But what if you could quantify the difference using physics and math?
Well, that’s just what my next guest did. Joining me to discuss how to quantify the beauty of vibrato, are Elaine Chew, Professor of Digital Media at the Center for Digital Music, and Khalid Rajab, Assistant Professor of Electrical Engineering at Queen Mary University of London. Welcome to “Science Friday.”
ELAINE CHEW: Thank you.
KHALID RAJAB: Hi, Ira.
IRA FLATOW: Thanks for joining us. I want to tell our listeners that if you want to see vibrato visualized with math, to go to our website at sciencefriday.com/strings. And I want to ask everybody, do you play the music yourself? Are you eager to analyze your own vibrato skills, or some other musical element you want to dissect with math? Give us a call. Our number, 844-724-8255. You can also tweet us @scifri.
Elaine, as a musician yourself, give us a layman’s explanation of what vibrato is.
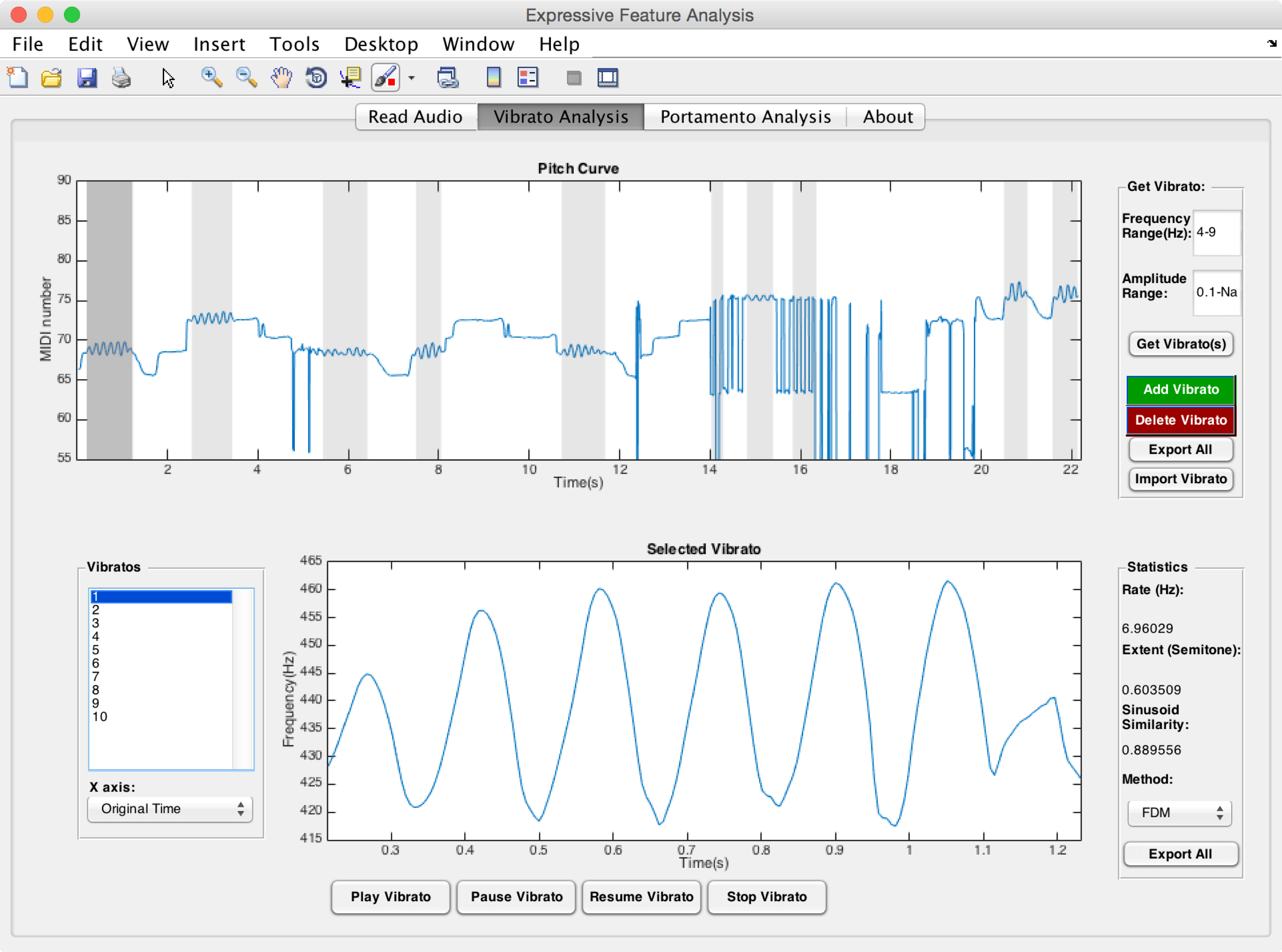
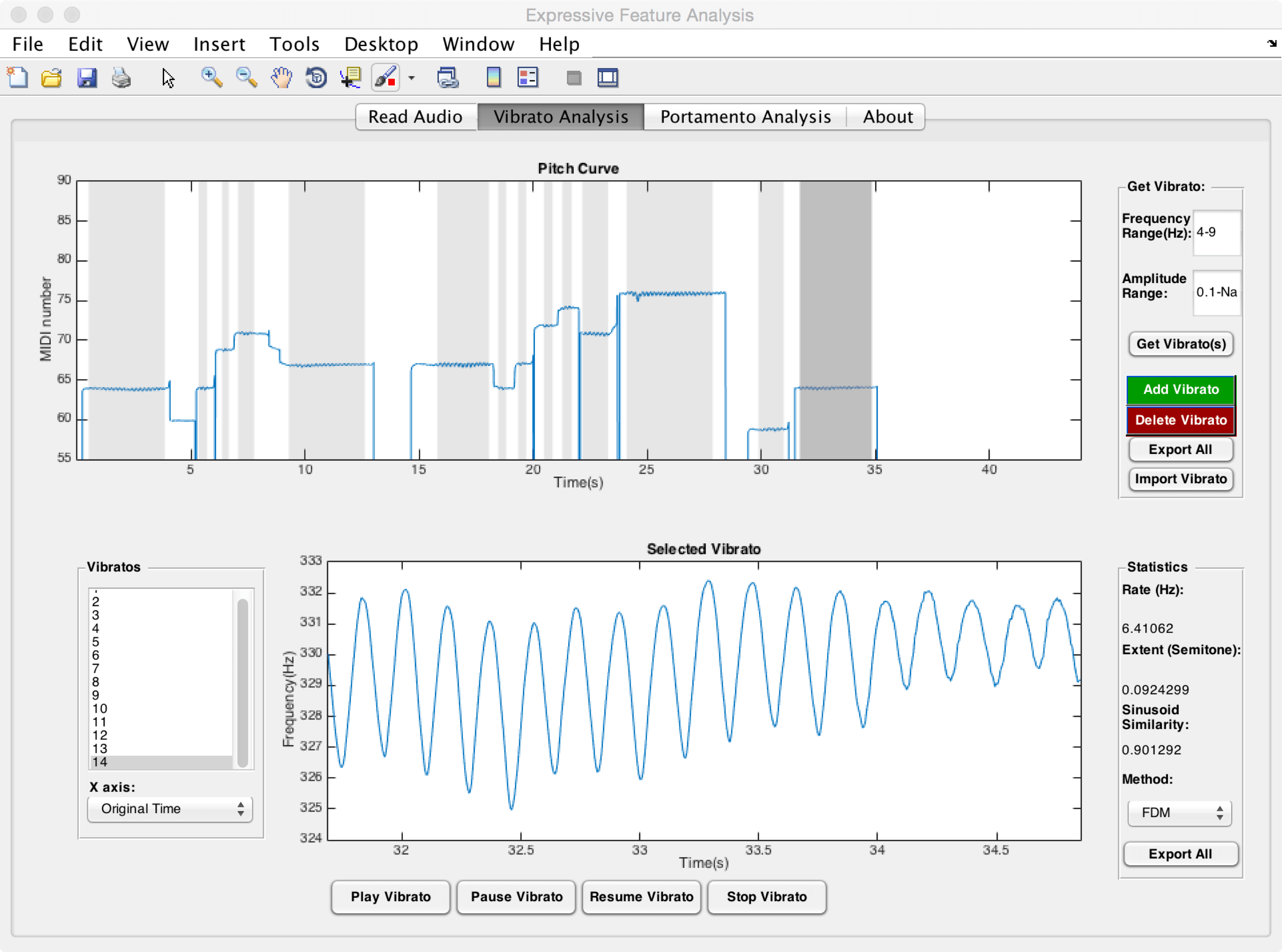
ELAINE CHEW: Well, vibrato is an oscillation of a tone. So if a tone is just played directly without any elaboration, it’s just a flat tone, and it just sounds very plain and simple. But when you add vibrato, it adds the richness to the tone, and it adds another dimension of expressivity that the performer can control, and shape, and therefore influence the listener’s emotion response.
IRA FLATOW: Now I know one of the goals of this project was to analyze the difference between the vibrato on the erhu, and a Western instrument like a cello or a violin. And we have a couple of sound samples. Let me play them first for us. First, the vibrato on a cello.
[CELLO PLAYING]
Quite beautiful. Now vibrato on the Chinese stringed instrument, the erhu.
[ERHU PLAYING]
Now that’s beautiful too. Wow. Khalid, what does the math of quantum physics have to do with music, and specifically, vibrato? How do you use it?
KHALID RAJAB: Yeah, I’m here. Can you hear me?
IRA FLATOW: Yes, I can hear you. Let’s talk about how you use quantum physics to analyze the music.
KHALID RAJAB: Yeah, sure. That’s a great question. And first of all, I’ll say that I have very little musical background myself. So I played a bit of piano when I was in school. But we can all appreciate the beauty of music. But I was really a lot more on the maths and the physics side of things.
But for me, if I’m looking at it from the perspective of mathematics, music is– it has a signal. So we can look at the audio, the amplitude, how loud it is, and how the pitch changes with time. And we can use very similar techniques, whether we’re studying physics, quantum mechanics, electromagnetics, or anything like that. And that’s where my background sort of came into it.
So I was looking at, basically, the oscillations of atoms. If we blast an atom with a magnetic field, we can create a resonance, so it’s going to start vibrating at one particular frequency. And those resonances are similar to what defines the pitch of music.
So if we’ve got a different note, or a vibrato is a frequency that’s changing with time, it’s oscillating. And so essentially, we’re using techniques that were developed for quantum mechanics, quantum dynamics, and applying those same techniques to look at different sorts of signals, So instead of quantum signals, we’re looking at musical signals. Although, I have to say, I mean, from my perspective, I’ve found it’s a lot more difficult to analyze the musical side of things than the quantum mechanics, just because I feel like you have so much more complexity just that’s input by the artist, by the musician, if that makes sense to you.
IRA FLATOW: Mm-hmm. So Dr. Chew, using all of these quantum physics tricks, what were you able to find out about the vibrato?
ELAINE CHEW: Well, first of all, we also need to credit the PhD student who did sort of a lot of the heavy lifting for this work. His name is Luwei Yang.
KHALID RAJAB: Yeah, absolutely.
ELAINE CHEW: And so actually, he ran a lot of the experiments, and found that the qualities of vibratos on the erhu were extremely different from the ones from a violin. And initially, we were studying the same piece of music when it’s performed on a violin versus on an erhu. And the piece was originally written for erhu. And so it has a very characteristic Chinese folksy sound. And when played on a violin, the violin tries to emulate that kind of folksy Chinese sound. And it gets close, but it’s not quite it.
And so he was able to extract exactly just how much more, how much wider the vibratos were. Were they faster, were they slower, sort of vibrato rates. Also looking at the shapes of the vibratos, whether they were shaped with one or two humps, whether it got wider, and then narrower, and then wide and narrow again. And so it was found that actually, it is true that the erhu, if you listen to it, the vibrato is much wider than on a violin. And part of the reason is because the violin, the instrument itself, has some physical constraints. [COUGHS]
IRA FLATOW: Dr. Chew, take a drink of water. Go ahead. No need for you to cough your way through this. Let me ask Khalid to follow up. It sounds very easy for our ears to hear the difference, right? I mean, between the two, we know immediately. Why is it such a challenge for a machine to do that?
KHALID RAJAB: That’s [INAUDIBLE].
IRA FLATOW: Are you there?
KHALID RAJAB: Hello?
IRA FLATOW: Yes, go ahead.
[INTERPOSING VOICES]
KHALID RAJAB: Yeah, I was saying at a very basic level, we’ve got a pitch, which is sort of like the frequency of the notes we’re playing. So you’ve got frequency, which represents and A, or a B, or a C, or C sharp, so on. And we can look at that pitch, and the computer can tell from that pitch what notes we’re playing. But it turns out that the notes can be a lot more complicated than that. And Elaine can actually tell you a lot more about this than I can.
But at the fundamental level, we’ve got not just the first frequency of the notes, but we have a lot more complexity, or richness to the notes. So we have the first frequency, but we have many other harmonics after that. And so the computer– it’s difficult first of all to pick out that frequency quickly enough so that it can analyze it in real time, but also to distinguish which is the correct frequency, and which frequencies are important, which frequencies are going to sort of trigger an emotion in us.
IRA FLATOW: Elaine, could we potentially unlock the secrets of the masters like Pablo Casals, using tools like this?
ELAINE CHEW: Well, we’re hoping that we can do that. Because the way that Pablo Casals probably uses vibrato is probably very different from another cellist, say, Yo-Yo Ma. And using these tools, we can not just listen to the quality of the vibrato, we can actually objectively quantify them. And if we’re able to objectively quantify them we can compare them next to each other. In a sense, we can freeze them in time, and look at the parameters that the artists evoke as they shape the vibratos.
And in so doing, we’ve taken something that is very much felt by listeners, and turned it into something that is not just about feeling. But we can actually see the shapes. We can actually quantify the parameters. And we can compare them with numbers, with mathematics.
IRA FLATOW: And Khalid, I only have about a minute or two left. But I know I have to ask you this question. I can’t let you go without asking.
KHALID RAJAB: Yeah.
IRA FLATOW: I understand you work on something any Harry Potter fan would love, and that is an invisibility cloak, is that right?
KHALID RAJAB: Yeah, that’s right. So a lot of my background was working on electromagnetics, so light, or radio waves. And something I’d been working on previously was– it’s called metamaterials. So it’s basically designing materials to behave how we want them to behave. And sometimes, this can in quite an unnatural way. So one thing that we’ve looked at is ways to design materials so they could bend light around objects, hence making them invisible.
IRA FLATOW: And so this has to do with resonance also.
KHALID RAJAB: Yeah, yeah, it is. And that can get very complicated within the structures, because you’ve got so many different materials that you basically design to resonate to different frequencies. And that opens up a whole host of problems, which scientists and engineers have to work on.
IRA FLATOW: We had a whole host of problems today, so that’s a good way. Thank you all for bearing with us this segment.
KHALID RAJAB: It’s the nature of international calls.
IRA FLATOW: It is. It’s a perfect storm. Elaine Chew, professor of digital media at the Center for Digital Music, and Khalid Rajab, assistant professor of electrical engineering at Queen Mary University of London. And you can check out our sound samples that we’ve been playing, and see for yourself.
We’re going to take a break. And coming up, the weather satellites we have to thank for alerting us to this week’s snowstorm. What might happen if they break? Scientists actually thinking about creating robots that might go up and fix the weather satellites. And you know how important the weather satellites are, wink, wink.
We’ll be right with you. Stay with us after this break.
Copyright © 2017 Science Friday Initiative. All rights reserved. Science Friday transcripts are produced on a tight deadline by 3Play Media. Fidelity to the original aired/published audio or video file might vary, and text might be updated or amended in the future. For the authoritative record of ScienceFriday’s programming, please visit the original aired/published recording. For terms of use and more information, visit our policies pages at http://www.sciencefriday.com/about/policies/
Katie Feather is a former SciFri producer and the proud mother of two cats, Charleigh and Sadie.
Christopher Intagliata was Science Friday’s senior producer. He once served as a prop in an optical illusion and speaks passable Ira Flatowese.