When ‘Proof’ Isn’t Enough

The following is an excerpt from Proof: The Art and Science of Certainty by Adam Kucharski.

When you purchase products through the Bookshop.org link on this page, Science Friday earns a small commission which helps support our journalism.

Buy The Book

Proof: The Art and Science of Certainty

Buy

Proof often carries a certain urgency. It is not just about what is true; it is about convincing ourselves—and others—that something is true. If prosecutors want to stop a murderer from walking free, they need to assemble enough proof to persuade a jury. If countries want to roll out a new vaccine during an epidemic, they need proof it’s sufficiently safe and effective. If we want to have fewer legal errors, or more medical advances, or make better decisions about whether to send up planes after a volcanic eruption, we need to seek out proof.

Yet our experience of proof can often feel fleeting and forced: here’s an established fact, remember it, recite it. In the early stages of my mathematics degree, it was drilled into us that we should never start a statement with “Clearly” or “Obviously.” If our logical steps are convincing, the reader should find them clear without us saying so. I’d later discover that writers have a similar mantra: “show, don’t tell.” But that still leaves us with the problem of choosing what to show, and how to show it.

Approaches to proof often depend on the situation we face. How would you show a new product is better than the old one? Or persuade a court of someone’s guilt? What would make you trust a self-driving car, or a financial transaction with a stranger? And which types of evidence would you want for an incoming government policy, or—if you were to be ambitious—the founding principles of a new country? Would you approach these questions like a philosopher, a lawyer, a computer scientist, or a statistician? Or someone else entirely?

Life is full of situations that can reveal remarkably large gaps in our understanding of what is true and why it’s true. This is a book about those gaps. It is the story of the ideas that have helped scientists and societies discern between truth and falsehoods, improving decision-making and reducing dangerous errors. From medieval juries to modern scientific revolutions, it is about the methods people have used to accumulate evidence, negotiate uncertainty, and converge on proof. And, crucially, what happens when those methods fail.

Furious letters flooded in from readers with PhDs. The target of their doctoral-level anger? Marilyn vos Savant, who held the record for the highest IQ in the world. It was September 1990, and vos Savant had just written a magazine column about a seemingly innocuous mathematical puzzle. Unfortunately for her mailbox, the solution she’d provided would cause an uproar. “May I suggest that you obtain and refer to a standard textbook on probability before you try to answer a question of this type again?” wrote one unhappy reader. “How many irate mathematicians are needed to get you to change your mind?” demanded another.

There would be thousands of letters in total, several of them on university letterheads. Many were patronizing: “Our math department had a good, self-righteous laugh at your expense.” Some went further, lamenting the harm she had caused to education: “There is enough mathematical illiteracy in this country, and we don’t need the world’s highest IQ propagating more. Shame!” Others decided the error lay in biology: “Maybe women look at math problems differently than men.”

The puzzle that had sparked such a furor was commonly known as the “Monty Hall problem,” after the US game-show host, and had been around since the 1970s, even though many mathematicians were evidently still unfamiliar with it. I would first hear about it as a teenager, a decade after the vos Savant controversy. But it would take me far longer to properly appreciate the puzzle’s implications.

If you haven’t come across the Monty Hall problem before, the premise is simple. You’re on a game show and must choose between three doors. Two doors have a goat behind them and the other a luxury car. You start by picking a door, say door number 2. Then the host, who knows what’s behind the doors, opens one of the other doors, say door number 3, to reveal a goat. He then gives you the option to switch your choice and pick door number 1 instead. Should you take up the offer?

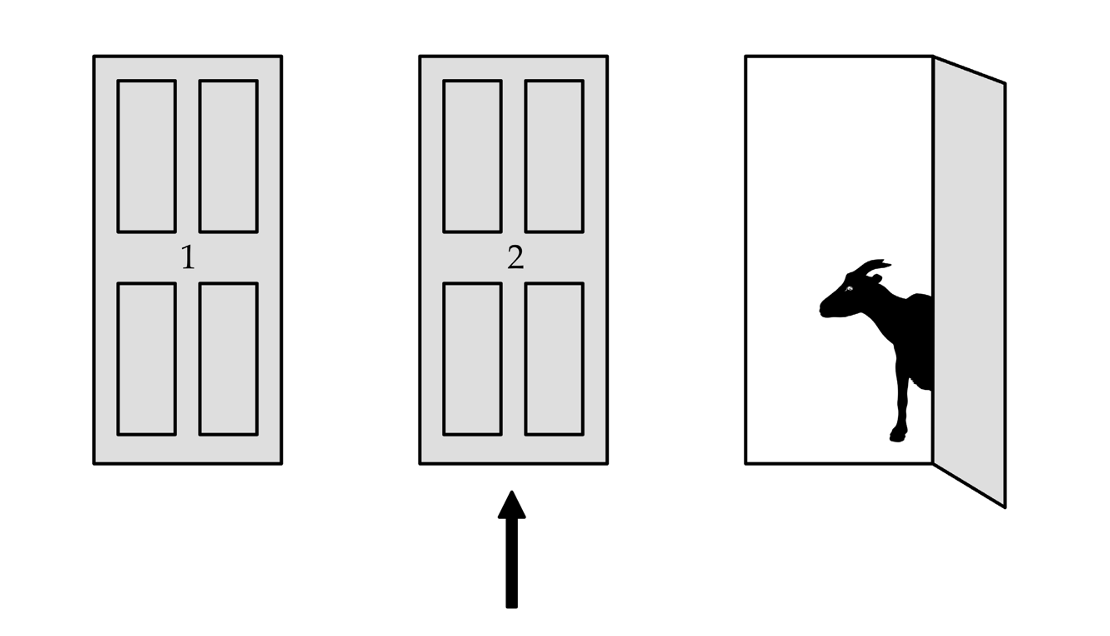
In 1995, mathematician Andrew Vázsonyi told his friend Paul Erdős about the puzzle. If anyone could work it out, it should be Erdős, who’d published more mathematical papers than anyone in the world and was a specialist in probability to boot. Would he switch, given the choice? Erdős said that “it should make no difference.” There were two doors left, he reasoned, so it should be a 50/50 gamble.

His response surprised Vázsonyi, who’d spent time working through all the combinations of possible choices, eventually deciding it did make a difference. For example, suppose the car is behind door number 1 and you correctly choose this door at first. If you later switch, you’ll lose the car. But now imagine you’d picked door number 2 instead. Remember that the host reveals a goat behind a door that’s not the one you chose. So in this scenario, it means the host opens door number 3. As a result, switching would win you the car. Likewise, if you’d picked door number 3 and the host reveals a goat behind door number 2, you’d win by switching. In other words, two times out of three you’ll get the car if you switch. The same logic holds if you think about what would happen if the car were behind another door initially. Vos Savant had given the same conclusion in her column: mathematically speaking, it’s better to switch.

Excerpted from Proof: The Art and Science of Certainty by Adam Kucharski. Copyright © 2025. Available from Basic Books, an imprint of Hachette Book Group, Inc.