Grade Level
6 - 8
minutes
15 min - 1 hr
subject
Mathematics
Activity Type:
geometry, math craft activity, transformations
What better way to impress your valentine than with beautiful mathematical patterns?
The human eye is naturally drawn to patterns, which is why repetitive designs adorn our homes and churches, printed fabrics and wallpapers are design staples, and dishes feature motifs of rotational symmetry.
With a little math, you can use hearts to create captivating and ornate graphic patterns perfect for making valentines!
Step 1: Make some hearts
It turns out there are lots of ways to make a heart, some more mathematically challenging than others. For some new ways to make hearts, check out this sweet heart-making instruction sheet. You can also print and cut out heart shapes and a coordinate plane to help make your heart patterns more efficiently. Take a look through the different ways to generate patterns below—some are easier to create with a whole set of identical pre-made hearts, while others work best if you draw a different heart each time.
Step 2: Transform your heart…over and over again
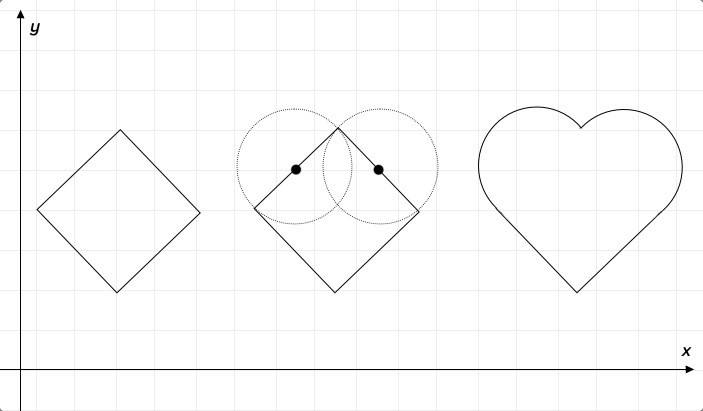
In geometry, transformation describes modifying the position, orientation, or size of a point, line, or shape. You can transform a shape by sliding it around on a coordinate plane (translation), rotating it (rotation), reflecting it across some line (reflection), or changing its absolute size (dilation). If a transformation is performed correctly, the resulting shape will look similar to the original shape, but it will be in a different position or be a different size from the original. By copying and transforming shapes repeatedly, you can make appealing patterns that naturally draw the eye to the similarity between the shapes.
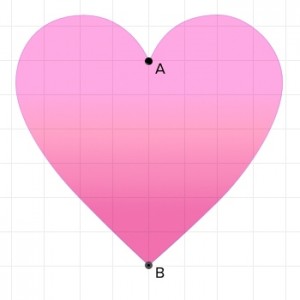
We’ll show you how to transform hearts by using two main points: point A, which rests between the two lobes of a heart, and point B, located at the heart’s pointy bottom.
Translation
Best performed by making a collection of pre-cut hearts or using a heart stencil

One fast way to create a pattern is to repeatedly copy and translate, or in other words, relocate identical heart shapes across space. To create a consistent pattern, translate each heart copy by the same amount each time you make a new heart. In the example above, each heart in a color series was placed two units up and two units to the right of the one before it. When you make your own pattern, it’s easiest to perform translations with a whole set of pre-cut hearts, or by using a heart stencil.
You can also perform translations on a heart using x- and y-coordinates. Just add or subtract a single number to or from the x- and y-coordinates of point A and point B. For example, say point B of a heart is located at (5, 0), and you want to translate it three units up and three units to the right. You would add 3 to that point’s x-coordinate value and 3 to its y-coordinate value to get its new position, like this: (5+3, 0+3) = (8, 3).
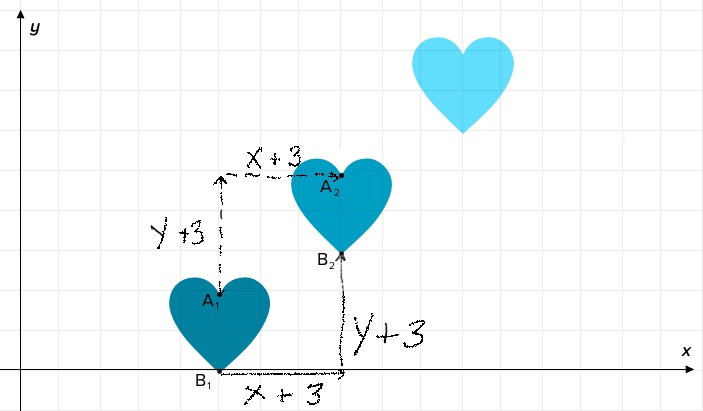
Challenge: In the above example, what are the original coordinates of point A, and what are the coordinates of point A after it has been translated?
Dilation
Best performed by using a ruler, a compass, and a pencil to draw hearts individually

Dilation is a very useful transformation for creating the appearance of hearts that are growing larger. Dilation changes the overall size of a shape, without changing the angles or relative sizes (ratios) of lines or curves that make up the shape. In other words, dilation resizes a shape so that it still looks like the original, just larger or smaller. You can dilate any heart by changing the distance between points A and B.
In the example of the red heart above, the distance between point A and point B for each consecutive heart increased by 30% compared to the heart before it. (For a 30% increase, multiply the distance between points A and B of the previous heart by 1.33).
You can also use x- and y-coordinates to dilate a series of hearts. Just keep point B in the same position while moving point A vertically with each additional heart. In the example below, point A of each heart (x, y) moved vertically one unit from the heart before it, changing its position to (x, y+1).
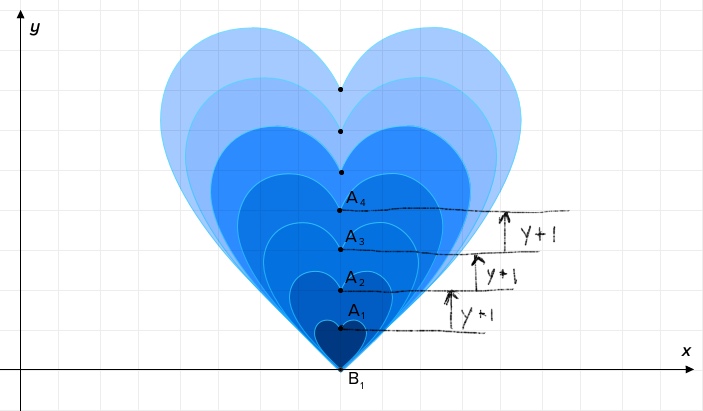
This type of transformation cannot be done with pre-cut hearts or stencils. To get the best dilation effect, you need to draw a new heart for each dilation, being careful to make your lobe sizes proportional. See the heart-making instruction sheet for help making consistent hearts.
Challenge: How would you change the x- and y-coordinates of the line if you wanted to make each subsequent heart twice the size of the first?
Reflection
Best performed by making a collection of pre-cut hearts or using heart stencils

Reflection is the ideal transformation for creating romantic pairs of hearts. Reflection is exactly like it sounds: shapes are reflected, or “mirrored,” across a straight line. Shapes are easiest to reflect across horizontal or vertical lines, as in the examples below. To perform a reflection, choose a “mirror line” (also called a line of reflection) that you will reflect your heart across. Measure the shortest distance between point A and the mirror line (the line of measurement should be perpendicular to the line of reflection), then repeat for point B. Next, recreate points A and B on the opposite side of the mirror line from the original shape, the same distances from the mirror line. Finish recreating your reflected heart using the new points as a guide.
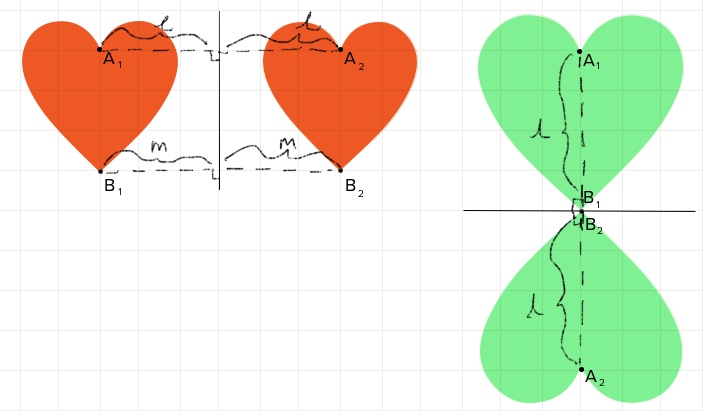
Challenge: Take a moment to plot the x- and y-coordinates of points A and B of a pair of reflected hearts. Are there patterns in how the coordinates of point A and B change with reflection that could help you generate future reflections? How do those patterns change if your mirror line is a line other than the x-axis or the y-axis?
Rotation
Best performed by making a collection of pre-cut hearts or using heart stencils
Do you want to try creating hearts that point every which-way, appearing to spin? Give rotation a try. Rotation involves taking multiple copies of one or more shapes and rotating them around a point of your choosing. Performing a rotation is easiest if you use a protractor and a ruler.
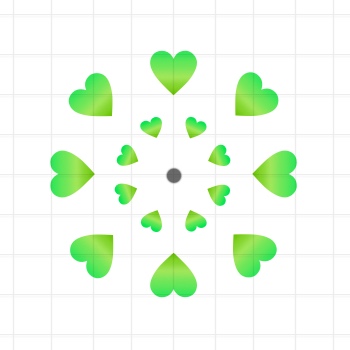
Start by drawing or pasting one heart on a piece of graph paper. Choose a point of rotation and use a ruler and a pencil to draw a line from your point of rotation to point A and point B in your heart (you’ll want to erase these lines when you are done). Use a ruler to measure and record the distances from the point of rotation to point A and point B. Next, use a protractor to measure a fixed angle from each of your lines, say 45° clockwise, and use your ruler to draw new versions of each line at that new angle, making sure each runs from the point of rotation. Lastly, draw or paste a new heart along the newly rotated lines, being careful to place it the same distance from the point of rotation as the original.
Repeat this rotation with multiple hearts to create a circular rotation pattern like the one above.
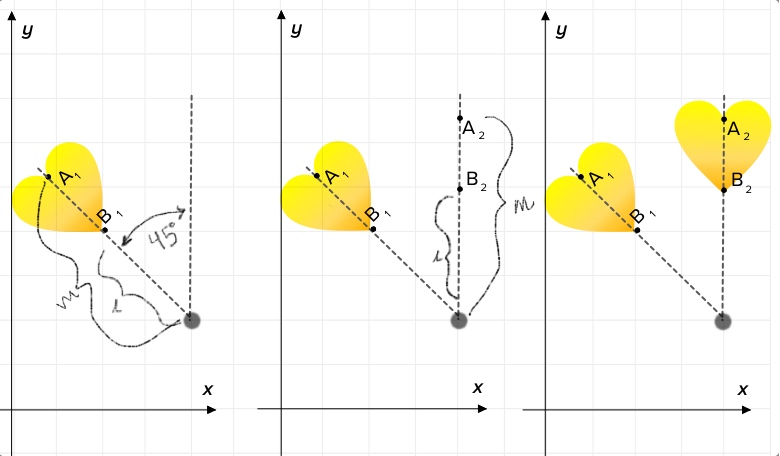
Challenge: How is rotation similar to and different from reflection?
Combine Multiple Transformations!
You don’t have to choose a single type of transformation to create your valentines. Use two, three, or four kinds of transformations at a time! For example, why not combine dilation, rotation, and translation, like in the example below?

Challenge: What combination of rotation, dilation, translation, and/or reflection was used to create the above image? How would you write directions to create the above image?
Get some inspiration from the math artists:
Ever heard of a math coloring book? To see real mathematical beauty, take a look at the pages of the book Patterns of the Universe, by math writer Alex Bellos and illustrator Edmund Harriss. “We think this is something that you can appreciate, knowing nothing about math,” Bellos told SciFri. “To me, it’s like an encyclopedia of amazing mathematical images that can be enjoyed for their aesthetic appeal—but can also be enjoyed to learn stuff.”
Teachers and educators can request a printable classroom packet via the book’s page here.
Coloring By Numbers, Mathematically
Math Is Beautiful
Teacher Tips and Standards
Teachers! Try these transformation tips
- Provide students with stencils of three similar hearts in small, medium, and large so that they can quickly trace transformations with a pencil, rather than re-creating them each time.
- For a beginner’s approach to translations, rotations, and reflections, have students cut out a collection of identical hearts that they can place on a piece of paper with a coordinate plane. Ask students to demonstrate each type of transformation using their heart cutouts.
- Before students start generating their valentines, invite them to first create patterns with heart cutouts, and ask them to describe how they made their patterns. Many students will have inadvertently followed a transformation rule to make their patterns!
Common Core Standards:
CCSS.MATH.CONTENT.8.G.A.1
Verify experimentally the properties of rotations, reflections, and translations:
CCSS.MATH.CONTENT.8.G.A.1.A
Lines are taken to lines, and line segments to line segments of the same length.
CCSS.MATH.CONTENT.8.G.A.1.B
Angles are taken to angles of the same measure.
CCSS.MATH.CONTENT.8.G.A.1.C
Parallel lines are taken to parallel lines.
CCSS.MATH.CONTENT.8.G.A.2
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
CCSS.MATH.CONTENT.8.G.A.3
Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
CCSS.MATH.CONTENT.8.G.A.4
Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
All images created by Ariel Zych for Science Friday.
Educator's Toolbox
Meet the Writer
About Ariel Zych
@arieloquentAriel Zych was Science Friday’s director of audience. She is a former teacher and scientist who spends her free time making food, watching arthropods, and being outside.