In 2016, math teacher and world traveler Bushra Makiya took a trip from Bronx, NY to Hamburg, Germany. While in Hamburg, she learned about the construction of the Elbphilharmonie, a new concert hall/community center that opened in November 2016. The construction of the building went way over budget, in part (she was told) because of the cost of the windows. Why were they so pricey? The windows were made with self-cleaning glass that eliminated the need for regular (and expensive) washing.

Was the self-cleaning glass worth the cost?

Let’s investigate the cost of window washing on large buildings like the Elbphilharmonie to determine whether the added cost of self-cleaning windows is worth it.

You’ve been asked to plan the construction of a new skyscraper. The board that commissioned it wants to know whether you think self-cleaning windows are worth the added cost. The board asks you to estimate the cost of window cleaning for the entire building to inform their decision. The skyscraper is 50 stories high and is going to be covered entirely by windows on all four sides. Each floor will have 38 windows. Once a year, all the windows will need to be washed. The cost for washing the windows is $2.00 for each first-floor window, $2.50 for each second-floor window, $3.00 for each third-floor window, and so on.

Can you figure out how much it will cost to wash the windows of this building every year?

There are lots of ways to figure out the annual cost of washing windows on this building. How would you start — or launch — the problem-solving process?

Bushra Makiya and Jon Koenig worked on ways to launch and work with students on The Skyscraper Problem as a part of a Math for America (MƒA)* Professional Learning Team (PLT). Check out some of the different launch options used some of those educators in our Educator Toolbox below.

It is daunting to think about manually adding up the costs of each of the windows on each of the floors individually for fifty floors of a building. Isn’t there a shorter or more efficient way to calculate the cost of window washing on a large building? It turns out this kind of math problem is a pretty old one, older even than skyscrapers. Let’s learn how it was first solved with a little story about a gentleman named Carl Gauss.

The story goes that when Carl Friedrich Gauss was in primary school, he constantly provoked the wrath of his teacher. To keep him busy, Gauss’s teacher told him to sum the consecutive numbers 1 through 100. His teacher was shocked when, seconds later, Gauss told him 5050 without having written anything down!

The mathematics behind this simple story are fascinating. Gauss noticed that in the numbers 1 through 100, there were 50 pairs of numbers that added to 101 (1 + 100, 2 + 99, 3 + 98, … 49 + 52, 50 + 51). He then multiplied that sum 50 times to reach the sum of the entire series, 5050.

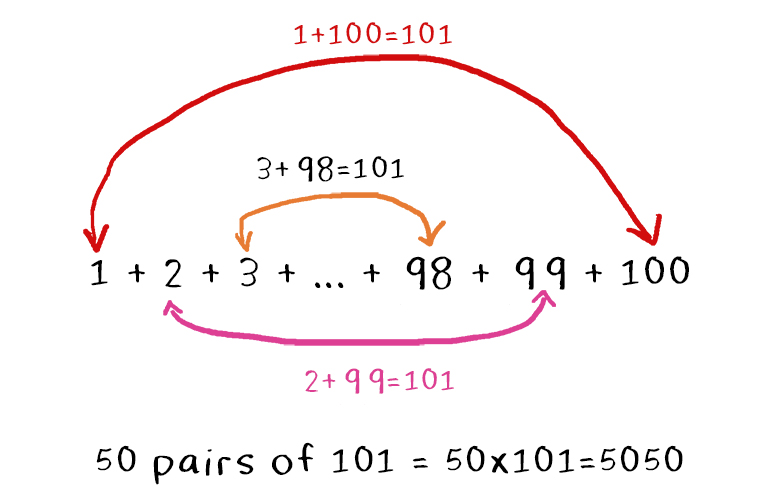
This timeless strategy of adding up consecutive numbers in a series by adding together pairs of numbers in the series proves useful in many problem-solving situations. Can you think about how it might be useful for calculating the cost of washing the windows of a large skyscraper? What is the consecutive number series in the skyscraper example?

---

First, let’s try a simpler problem.

If you’ve never seen consecutive sums before, it might help to start out with a simpler problem before approaching The Skyscraper Problem. When Bushra and Jon collaborated on this problem with other teachers, they found that thinking about a similar but simpler problem, like building stairs from blocks, helped get students ready to tackle The Skyscraper Problem. Here’s what they did.

After launching the problem, Bushra and Jon usually give students 20-30 minutes to work in small groups. Try either of the problem-solving strategies below to help figure out the total cost of the Skyscraper.

Strategy 1: Make a Table

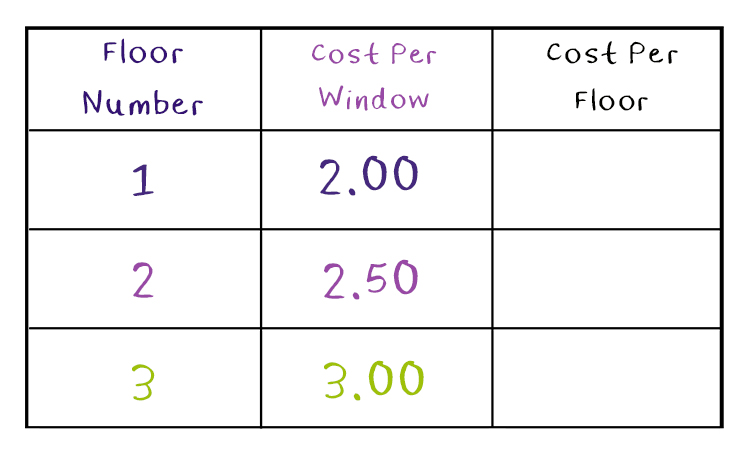
Strategy 2: Solve a Simpler Problem

It often helps to break down a big down a problem into smaller problems. Use the following guiding questions to help you.

1. How much will it cost to wash all the windows of the first three floors?

2. How much will it cost to wash all the windows of the first four floors?

3. If the building was 10 stories tall, how much would it cost to wash all of its windows?

4. How much will it cost to wash all 50 stories of this building?

5. Write a formula that shows how much washing the windows would cost if the building was n stories tall.

Consecutive Sums

Could you see the consecutive numbers in the Skyscraper Problem? Well, they’re not technically consecutive anymore, but we can still apply Gauss’s strategy.

To do this, it helps to look at the costs of window washing the bottom and top floors. But how much do the top floors cost? We’ll have to look at the pattern in the cost as the floor number increases.

Since each higher floor increases in price per window by $0.50, the cost of washing windows increases at a constant rate of change. We could use the linear expression 0.5n + 1.50 to find the price of a window on any floor, where n is the floor, $0.50 is the price added per floor, and $1.50 is the “starting price” – the baseline cost before we start moving up floors. To determine the cost of washing windows by the floor instead of by the window, we can multiply this expression by the 38 windows per floor, by multiplying by 38. So the cost per floor of washing windows on any floor is can be modeled by the expression 38(0.5n) + 1.50.

Using this, we can find the cost of washing windows on the top three floors:

• 38(0.5(48) + 1.50) = 969
• 38(0.5(49) + 1.50) = 988
• 38(0.5(50) + 1.50) = 1007

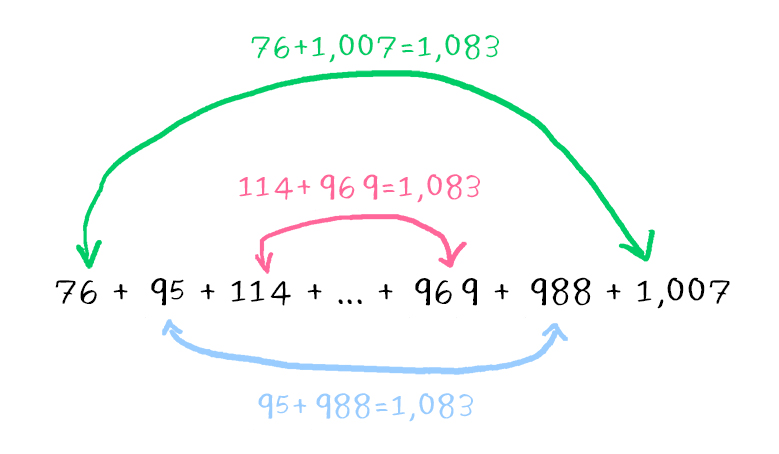
You should be able to take it from here! Remember how we applied this concept to Gauss’ problem and the staircase problem. How many pairs will you have, total?

Extension

• Self-cleaning glass costs 20% more than regular glass.  Does this change your answer about whether or not self-cleaning windows are worth the added cost?  Why or why not?
• Why does Gauss’s strategy work for the skyscraper problem, even though the costs per floor are not consecutive integers?
• In what other situations that use consecutive numbers could this strategy be beneficial?

Using Quadratic Equations

Depending on your students’ experience with quadratics, some students may add a fourth column to their table and use this to write a quadratic equation for the total cost of washing n floors.

Using Second Differences to Write a Quadratic Equation

Similar to the way linear equations can be written by finding the constant rate of change, you can find a quadratic equation from a table of values by using a method called second differences. Click here for a quick review.

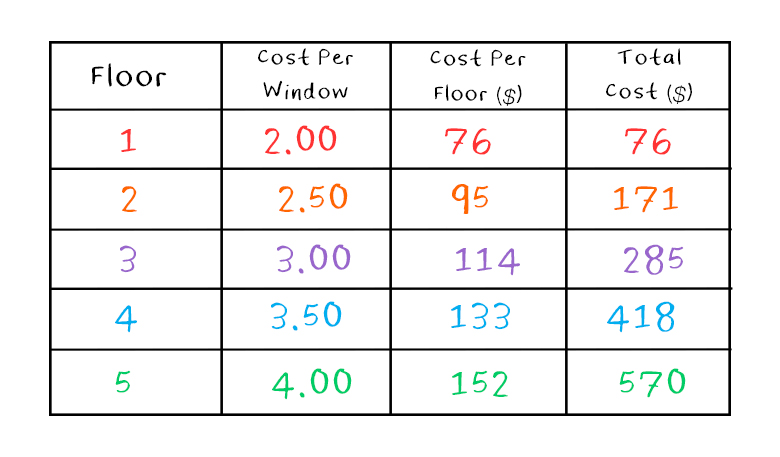
First, let’s recreate our table of values to focus on the total cost as a function of the number of floors.  We can also add a row for a “zero-floor” building to allow us to calculate the y-intercept.

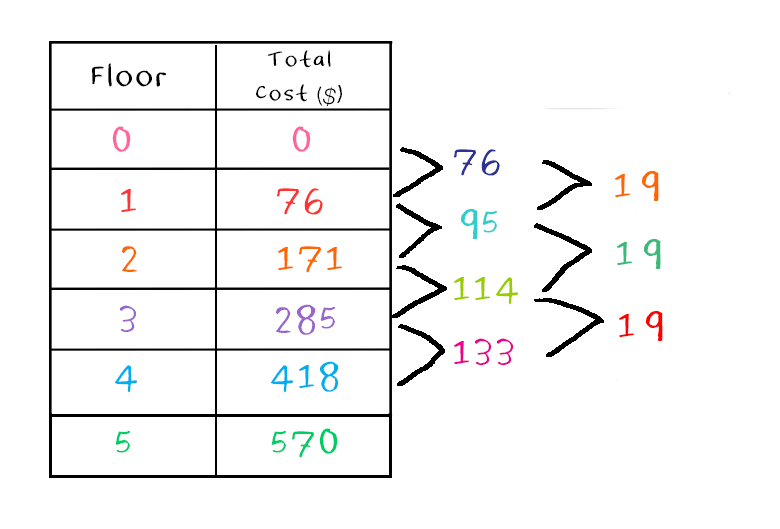
A standard form of a quadratic equation is written as y = ax² + bx + c.  The method of second differences tells us that 2a must be equal to 19.  Can you take it from here?

If you need a bit more help, see the rest of the solution here.

Extension Question: Can you use your formula to check the total cost of a 10-floor building? To check the cost of a 50-floor building? To find any other costs?

Using Average Cost to Find the Total Cost

You can also predict the total cost of skyscraper window washing by finding the average cost per window and then multiplying by the total number of windows in the building.

The cost of washing a single window grows linearly with each additional floor, which, as we learned before, can be expressed by 0.5n + 1.50.   To calculate the average cost per window, we must calculate the average of the first and top floor windows:

— Average cost per window = (cost per window first floor + cost of per window nth floor)/2

Each floor of our skyscraper has 38 windows. The total number of windows can be expressed as 38n.

Now that we have an average cost per window and the total number of windows, we can calculate the total cost:

Total cost = total number of windows * average cost per window

Extension question: Can you show that this formula is equivalent to the one you found using second differences?

---

Odd Number Challenge

We just worked with an even number, now let’s imagine you want to estimate the cost of window washing for a skyscraper that is 45 stories high. Each floor has 38 windows per story. Which of the three approaches — consecutive sums, quadratic equation, or average cost — would you use to find the total cost?

 

Bushra Makiya, MƒA Master Teacher
Bushra teaches at The Leadership & Community Service Academy, a public middle school in the Bronx. Bushra has been a teacher of mathematics for thirteen years and is in her 9th year of her MƒA Master Teacher fellowship. She is also a New York State Master Teacher and won the New York City Big Apple Award for Excellence in Teaching in 2016.

 

 

Jon Koenig, MƒA Master Teacher Jon teaches at Washington Heights Expeditionary Learning School (WHEELS), a public high school in Manhattan. Jon has been teaching mathematics for the last 10 years and is in his 4th year of his MƒA Master Teacher fellowship. He was also a finalist for the Klingenstein Teacher Award in 2016.

---

MƒA Professional Learning Team (PLT)

The Skyscraper Problem above was explored in a learning format known as a PLT, which is one of the many professional development formats implemented at Math for America (MƒA) with teachers in their community. MƒA PLTs are made up of small teams of teachers (about 15) who meet over a sustained period to collaboratively learn, reflect, and share classroom ideas and best practices. Always co-facilitated by two teachers, these PLTs have several guiding principles and an overall goal of examining teaching practice, research, and application.Learn more about MƒA PLTs here.

This particular PLT was called Problem Solving Cycle: Doing and Implementing Rich Math Tasks in Algebra. [This activity is originally adapted from Fostering Algebraic Thinking: A Guide for Teachers, Grades 6-10.]

MƒA builds a community of accomplished mathematics and science teachers, providing them with multiple opportunities for collaboration and continued learning, so they stay in the classroom and make the greatest impact. MƒA fellowships for outstanding mathematics and science teachers are different than any other across the nation. Learn about the power of the MƒA community at MathForAmerica.org.

*Math for America is an occasional sponsor of the Science Friday podcast.

Standards

• HSA.SSE.A.1: Interpret expressions that represent a quantity in terms of its context.*
• HSA.SSE.A.1.A: Interpret parts of an expression, such as terms, factors, and coefficients.
• HSA.SSE.A.1.B: Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret P(1+r)n as the product of P and a factor not depending on P.
• HSA.CED.A.1: Create equations and inequalities in one variable and use them to solve problems.
• CC PRACTICE STANDARDS
  1. Make sense of problems and persevere in solving them.
  2. Reason abstractly and quantitatively.
  4. Model with mathematics.
  8. Look for and express regularity in repeated reasoning.

Illustrations and photos (uncredited above) created by Xochitl Garcia for Science Friday.