Have Yourself A Mathy Little Christmas
Tips for a geometrically superior holiday season.
The following is an excerpt from The Indisputable Existence of Santa Claus by Hannah Fry and Thomas Oléron Evans.
First things first—before your Christmas planning gets under way in earnest, you’ll want to get off on the right foot with a geometrically superior Christmas tree.
In some senses, designing the perfect tree is simple. All you need is a neat, symmetrical placement of garland and lights, accented by an equally precise arrangement of spectacular twinkling ornaments.
Related Segment
How Can Math Make Your Holidays Merrier?
But how long does your garland or string of lights need to be to wrap around your tree perfectly? Rather than relying on guesswork, there is a simple equation you can use to help you.
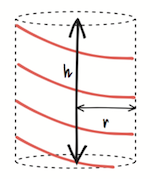
To give you an idea of all the festive glory you can hope for with this calculation, we’ve included a sketch of your tree on the right.
You did buy a cylindrical tree, right?
Even if you didn’t, this version of the formula works for particularly fat Christmas trees that are approximately cylinders, save for the spindly bit at the top which you don’t cover in garland anyway.
In red is the garland wrapped around the tree. The height of the cylindrical section is h and the radius is r. If you unravelled the cylinder to look at only the surface of your Christmas tree, it would look something like the following: a rectangle of height h and width equal to the circumference of your tree, 2πr.
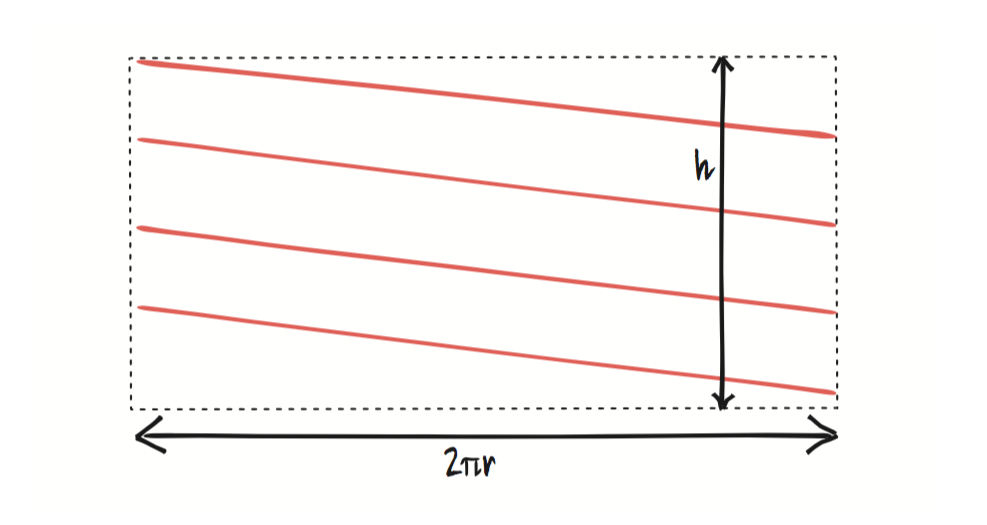
The diagonal lines represent loops of garland around your tree. As each line disappears off the edge on the right-hand side, it appears as the beginning of the next diagonal line on the left—like a pine needle PAC-MAN.
Exactly how many loops your tree should have we’ll leave to your artistic talents, but once you’ve made your decision (let’s say you have n loops), the length of the garland can be easily calculated by zooming in on one of these diagonal lines.
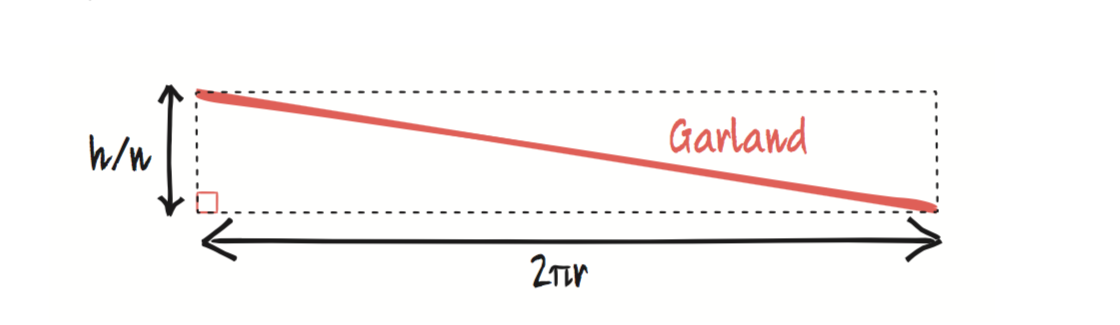
Since you want everything to be evenly spaced, the vertical distance each loop must cover is h/n. The width is just the circumference of your tree, 2πr, and, since the length l of the garland on this particular loop forms the hypotenuse of a right-angled triangle, Pythagoras does the rest for us:
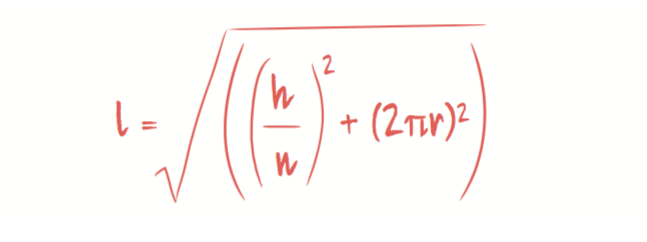
Who said Pythagoras would never be useful?
Taking all n loops into account, the total amount of garland required, L, is given by the following formula.
“But hang on!” we hear you cry. “My tree isn’t cylindrical!” If anything, it looks more like a cone. Typical mathematicians making sweeping unjustifiable assumptions…
Well, hold on to your accusations for now. While you can use the cylindrical version as an upper limit on your required amount of garland, even if your tree gets a lot skinnier at the top, we’ve also done the calculation for a tree that takes the more traditional shape of a cone.
The math isn’t for the faint-hearted, but if you’re keen not to waste garland you can find the equation in the book.
The Indisputable Existence of Santa Claus: The Mathematics of Christmas
For the rest of us, happy with our geometrically dubious trees, we can move on to the matter of ornaments. Spherical ornaments seem to be the traditional decorations with which to adorn a tree and in any other setting we’re big fans of spheres. But while they may catch the light rather beautifully, to a mathematician they’re just not very…festive.
If we’re being honest with ourselves, we can all agree that there is nothing more Christmassy than corners.
Not just any corners, of course. We want neat, symmetrical, mathematically superior corners. Which is why, for our tree decorations, we’re turning to our five favorite shapes; objects that have been admired and studied by geometers for thousands of years.
Ladies and gentlemen, may I introduce you to…The platonic solids:
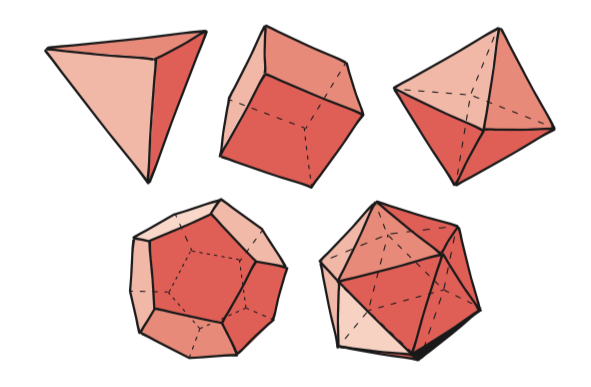
The platonic solids are 3D shapes where every face is a regular polygon. Around a face, every side is the same length and every angle is the same size. Looking at each shape as a whole, every face is identical and every corner is the same as every other.
Our platonic solids are: (top row, left to right) the tetrahedron, the hexahedron (which often goes by its street name of “cube”), the octahedron, (second row) the dodecahedron, and the icosahedron.
These five beauties are the only three-dimensional shapes that fit our criteria. We know this, not because we’ve checked all possible three-dimensional shapes, but because we can prove it. To find out how, you’ll have to read the book.
Any of these five platonic solids would look marvellous on a mathematical Christmas tree. After careful consideration, we reckon the hexahedron offers the perfect aesthetic balance between simplicity and cornery goodness.
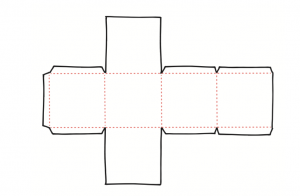
You can make your cubic ornaments using the template to the right.
With your tree bedecked with fantastically festive Christmas cubes, you’re sure to be the talk of the town.
Hmm…For some reason, our editor seems to think that cubical ornaments are insufficiently ambitious. Well then, in case you also can’t appreciate the supreme elegance and mathematical purity of the cube, we’ve put together some instructions for making your very own stellated icosahedral ornaments.
The icosahedron is the basis for this shape. Technically, a stellation is where you extend out the planes of each face until they meet beyond the boundary of the original shape. In this case, it’s just like adding a point to each of the faces of your icosahedron.
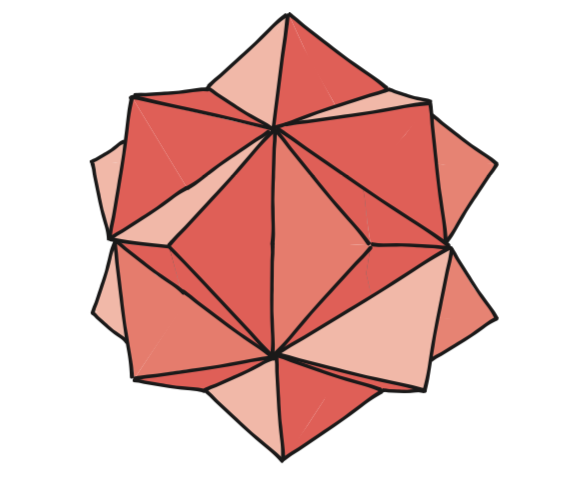
The end result here is a 20-pointed three-dimensional star that will look superb as a sparkling ornament or, when supersized, perfect taking the place of pride at the top of your tree.
Here’s how to make it.
This origami-style technique involves making a series of modules from smaller pieces of paper and then slotting them together to create the final shape.
You need to start off with a square piece of paper. Some people suggest using Post-it notes, others recommend tinfoil, but for that extra Christmassy glitz, we think metallic wrapping paper is the way to go.
Related Segment
Super Strong Robot ‘Muscles’ Inspired By Origami
Related Segment
DIY Holiday Gift Hacks
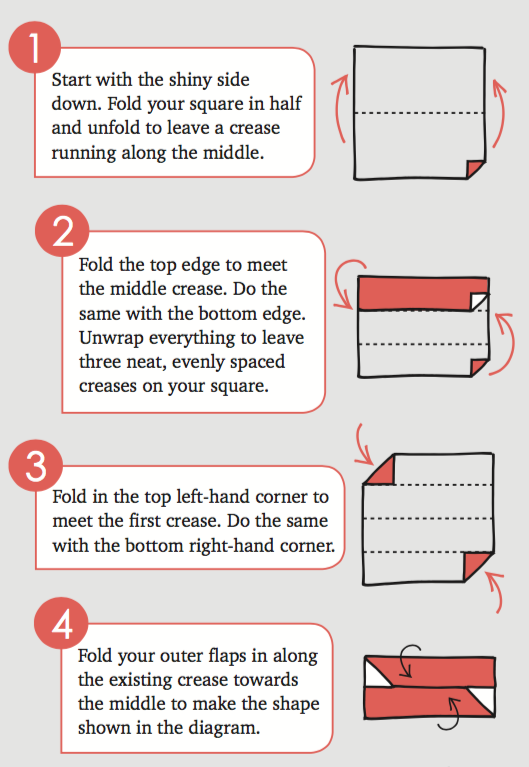
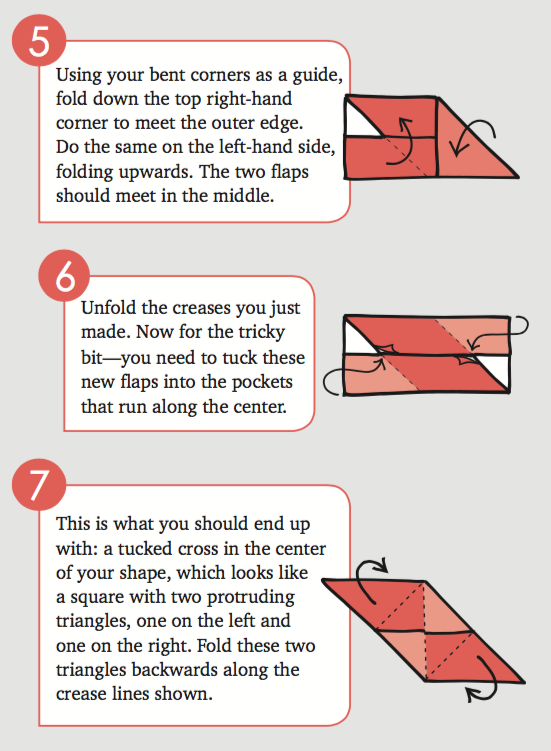
Carry on slotting modules together in the same way, securing with glue if necessary, until all 30 are in place. The final few will be a little tricky, but the shape of the icosahedron should emerge naturally from the creases in the paper.
And there you have it. Simply repeat this entire process 20 or so times to create 600 modules which will slot together for a complete set of ornaments, plus 30 more with larger squares of paper for the star on the top of your tree. And, assuming it’s still December, you’ll have a festive centerpiece bedecked in mathematically glorious decorations that will be the envy of all of your friends at your Christmas party.
At which point you can just sit back, add some ice regular hexahedrons to your rum punch, and marvel at your creation.
Adapted from The Indisputable Existence of Santa Claus by Hannah Fry and Thomas Oléron Evans. Copyright © 2016, 2017 by Dr. Hannah Fry and Dr. Thomas Oléron Evans. Published in 2017 by The Overlook Press, Peter Mayer Publishers Inc. www.overlookpress.com. All rights reserved.
Meet the Writers
About Hannah Fry
@fryrsquaredHannah Fry, Ph.D., is a lecturer in the Mathematics of Cities at the Centre for Advanced Spatial Analysis at UCL, and is co-author of The Indisputable Existence of Santa Claus (The Overlook Press).
About Thomas Oléron Evans
@MathistophelesThomas Oléron Evans, Ph.D., is a Teaching Fellow for the Smart Cities and Spatial Data Courses at the University College London, and the co-author of The Indisputable Existence of Santa Claus (The Overlook Press).