Fibonacci Sequence—A Handy Mathematical Approach For Looking At Evolution!

What Is A Fibonacci Sequence?

Patterns are found all over the natural world. From the grasping tendrils of a plant to the dew-laden web of a spider, we can see repeated sequences as a product of living systems. One pattern we will focus on in this resource is the Fibonacci sequence. The result of the sequence creates stunning swirls and grasping hands. As you watch the following video to observe its beauty and mathematical importance, think about these two questions:

1. Can you describe the pattern that was discussed in the video?
2. Dr. John Edmark talked about the golden ratio appearing in nature. Where did he say that it appears? Can you think of other places where it might appear?

The pattern described in the video is called the Fibonacci sequence. The Fibonacci sequence is named after Leonardo Fibonacci, an Italian mathematician who wrote about the pattern in his journals as he observed how rabbits reproduce.

The Fibonacci sequence works like this.

Let’s say you have two segments of a specific length, A and B, where A is bigger than B.

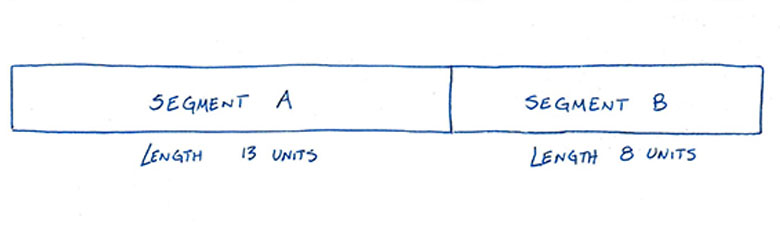
If these two segments are in a Fibonacci sequence, the bigger piece divided by the smaller piece will be approximately 1.618.

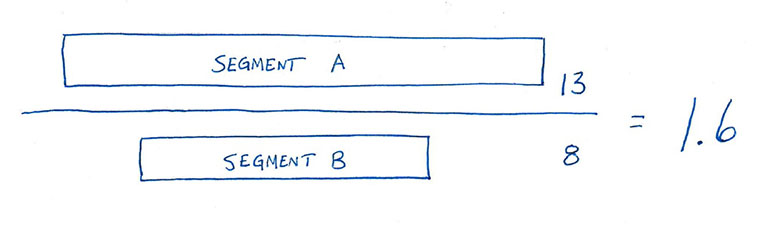
Also, if you take A’s length and add it to B’s length, then divide by A’s length, you will get the same number: 1.618. This ratio is called the golden ratio.

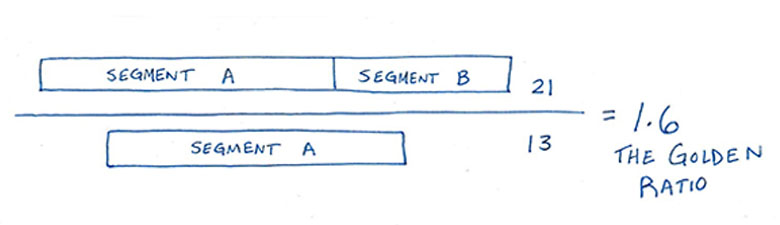
For example, the following numbers are a Fibonacci sequence: 3, 5, 8,13, 21, 34, 55, etc. When we divide 5 by 3 we get about 1.6. Divide 8 by 5 you also get about 1.6. 13 divided by 8? About 1.6 again!

To determine the next number in the sequence, you simply sum together the previous two numbers. You can repeat this process to generate an infinitely long Fibonacci sequence. For example:

If you select any three numbers in a row from a Fibonacci sequence, you’ll find the same pattern. Let’s define Fn as any number in the sequence, and then define (n-1) as the number positioned just before Fn, and (n-2) as the number two positions before Fn in the sequence. For any Fibonacci sequence, Fn will always be equal to (n-1) + (n-2).

For example, let’s look at a Fibonacci sequence starting with 75, 120, 195. To find the next number in this sequence (Fn), you can add 120 (that’s the n-2) to the 195 (the n-1) to get 315 (the Fn). So the sequence is now is 75, 120, 195, 315. You now have a Fibonacci sequence!

The ratio of the bigger number divided by the smaller number, that always equals 1.6, is denoted by the Greek letter Phi (Φ) and is called the Golden Ratio. You can find Phi in the above Fibonacci example: 315 / 195 = 1.615.

If you put rigid pieces of wood, measured in lengths of several successive Fibonacci sequence numbers together end to end in this pattern, you will see the additive effect observed in the video where Dr. Edmark’s structures curl beautifully in on themselves.

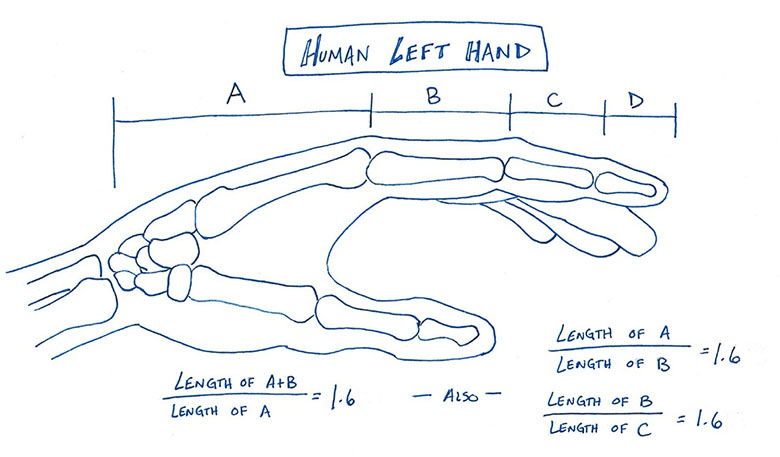
The Fibonacci pattern can be found all over in nature, like in the formation of a nautilus shell, the swirl of a hurricane, and the petal distribution of a flower. It can also be found in your very own hand. 

Look at your hand. Each of your fingers has three bones in it called phalanges (phalanx for singular). When you measure the length of the phalanges in order from the wrist to the tip of each finger, you will find that the sequence of lengths is pretty close to a Fibonacci sequence. Is it possible that this arrangement of phalanges is helpful or adaptive in some way for gripping objects?

You are going to figure out the optimal phalange arrangement needed to grasp a variety of different shaped objects by modeling a grasping hand with different phalanx lengths. Given a set of pre-determined phalanx lengths, you will create a “finger” and evaluate how effectively that finger grasps different objects. You will create multiple models of only the index finger of a hand and determine which formation allows for the maximum surface area contact with the most of the given objects. Use this printable handout to model the grasping hand.

Be sure to graph the data of your final model. You will use this graph as you move onto the next section.

Here are templates for some of the cardboard pieces you will need for this lab.

• Cardboard strips approximately 6.5 cm wide (represent the bones)
• Precut these cardboard strips into designated lengths for each lab group
  • 4x 20.5cm
  • 4x 12.5cm
  • 4x 7.5cm
  • 4x 5cm
  • 4x 3.5cm
• Hole punch
• Flat cardboard circles and squares (use template as patterns)
  • Circle with a diameter of 5.5cm “X”
  • Circle with a diameter of 15cm “W”
  • Square with a length of 5.5cm “Y”
  • Square with a length of 2.5cm “Z”
• 6 x 1/2 cm chenille stems as ligaments to hold the bones together

Models are all great and dandy, but is the Fibonacci sequence actually visible in the “hands” of other animals? Let’s take a look at how animals bones match up to the Fibonacci sequence.

For each hand, measure the length of each of the bones of the index finger (three total) and the metacarpal/carpal combo (4th measurement) for each species hand. Use this Analyzing Forelimbs of Various Animals worksheet for directions and as a place to record your results. 

The goal is to measure and predict whether the X-ray of the given organism’s hand would be a good grasping hand. If it is determined that the animal’s hand would not be a good grasping hand, a group discussion should follow as to what that hand could be used.

Click the images below to access PDFs of X-rays for printing and measurement:

The phalanges in humans hands are sized similarly to a Fibonacci sequence, and our hands can grasp objects well. Our baby fingers measure closest to a Fibonacci sequence. Most primates are great graspers as well and are evolutionarily related to humans. The best part of looking at all of these X-rays is that you can see that all animals, even ones that aren’t primates or mammals, have the exact same bones in the exact same order. The bones are just in different size proportions, and may perform a different function for that organism.

There are many different hands found in nature that are all so different, but clearly some are more similar to one another than others. A reason for some of these similarities is that some organisms are more closely related evolutionarily, meaning that they share a more recent common ancestor.

Let’s look at a phylogenetic tree to compare the different species in the X-ray analysis. Phylogenetic trees are representations that show the evolutionary relationship between organisms. They are constructed using the similarities and differences in genetic, anatomical, and physiological information. For more information on how to interpret a phylogenetic tree please refer to University of California Berkeley’s website.

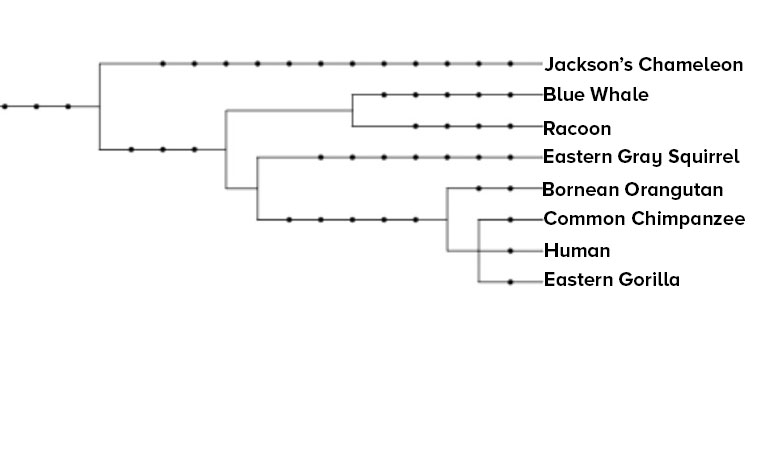
Observe the tree above and the common names of each species. Answer the questions below.

1. When you look at the phylogenetic tree above, locate animals that you might consider to have good grips. Are the animals with good grasping ability near each other? When organisms are close to each other on a phylogenetic tree, they are more evolutionarily related. What else could you predict about the organism’s anatomy and physiology because of this relatedness?
2. Hands for grasping aren’t exclusive to primates. Observe the chameleon hand in the picture below:

   

   Based on the picture do you think that a chameleon would be good at grasping? What kind of bone arrangements would you expect in this chameleon’s hand? Why?

   Carefully consider where the chameleon is on the phylogenetic tree. Would you say that the digits used by the chameleon to grasp are homologous structures or analogous structures to the digits used by the human hand to grasp? Could it be both? Defend your answer.

   Now that you’ve taken some time to look at Fibonacci sequences, and ways that the Fibonacci sequence can be used, be on the look-out for more examples of this amazing occurrence in the world around you!

HS-LS4-1
Biological Evolution: Unity and Diversity. Communicate scientific information that common ancestry and biological evolution are supported by multiple lines of empirical evidence.

HS-LS4-4 
Biological Evolution: Unity and Diversity. Construct an explanation based on evidence for how natural selection leads to adaptation of populations.

MS-LS4-6
Natural Selection and Adaptations. Use mathematical representations to support explanations of how natural selection may lead to increases and decreases of specific traits in populations over time

Crosscutting concepts addressed:

• Patterns
• Cause and Effect
• Structure and Function
• Systems and System Models
• Scale, Proportion, and Quantity

Evolution by natural selection states that organisms that are better adapted for the current environment will have a better chance at surviving and reproducing. The result is that those individuals with the better traits will reproduce more, and more offspring with the heritable, beneficial traits of their parents will make it into future generations. We can find a wide variety of patterns among organisms that are a result of evolution by natural selection. The Fibonacci sequence and the curl of a hand for grasping is potentially one example of an evolutionarily generated pattern.

To be able to wrap a set of fingers around an object is great, but in order to be able to manipulate objects in a wide variety of environments, animals may need additional structures to help them maintain a grip. The opposable thumb is one such structure, but primate hands may have another bonus gripping adaptation: Finger wrinkles.

Watch this Science Friday video about a trait that is present in primates.

For more help and a way to see it connected to evolution, take a look at these SketchNotes.

Convergent evolution leads to analogous features. An analogous feature is one in which the feature may look like another feature but this similarity is more due to a similar habitat or niche. An example of this is a butterfly wing and a bat wing. The similarity of these two organisms is due to the similar niche of moving through the air using flight as their main source of locomotion. Divergent evolution will produce homologous structures. Homologous structures appear in different animals but are very similar in makeup due to recent common ancestors.

Want to try to make your own phylogenetic trees? When you use the following directions, you will be able to compare virtually any living organism to any other organisms and see their evolutionary relatedness. All DNA that is used in these trees has been loaded in by scientists that study that particular organism and is housed at NCBI (National Center of Biotechnology Information).

Use this guide to create your own phylogenetic tree.

Hamilton, R., & Dunsmuir, R. A. (2002). Radiographic assessment of the relative lengths of the bones of the fingers of the human hand. Journal of Hand Surgery, 27(6), 546-548.

Hutchison, A. L., & Hutchison, R. L. (2010). Fibonacci, Littler, and the hand: a brief review. Hand, 5(4), 364-368.

Jouffroy, F. K., & Medina, M. F. (2002). Radio-ulnar deviation of the primate carpus: An X-ray

study. Zeitschrift für Morphologie und Anthropologie, 83, 275-289.

Littler, J. W. (1973). On the adaptability of man’s hand (with reference to the equiangular curve). Journal of Hand Surgery, 5(3), 187-191.

Park, A. E., Fernandez, J. J., Schmedders, K., & Cohen, M. S. (2003). The Fibonacci sequence: relationship to the human hand. Journal of Hand Hurgery, 28(1), 157-160.

Illustrations: Jeff Grant
Editing: Shirley Campbell, Ariel Zych
Digital production: Brian Soash, Brandon Echter, Daniel Peterschmidt, Ariel Zych