If you’ve ever played with tops, you know that some spin easily while others wobble. Ever wonder why?

The answer has to do with rotational inertia, a property shared by all rotating systems. Sometimes referred to as the moment of inertia, rotational inertia describes an object’s resistance to a change in its rotation. You experience and observe rotational inertia in many everyday activities, like when you swing a heavy baseball bat, for example, or when you push a lot of people on a merry-go-round.

Engineers must take rotational inertia into account when designing products that involve spinning. For instance, rotational inertia can affect how much power an engine can deliver to a vehicle to increase its acceleration, and how well propellers perform in the air and in the sea. It is even a crucial consideration in designing tennis rackets and golf clubs.

To start a top spinning, you have to apply torque. The amount of torque you must exert depends on the top’s rotational inertia. As you might have noticed, tops tend to be shaped in similar ways. Why do you think tops have such distinctive shapes?

Rotational inertia is defined by the distribution of an object’s mass relative to the axis of rotation. When thinking of an object’s distribution of mass, imagine that the object consists of a bunch of tiny cubes. The distance of each of those cubes from the axis of rotation affects how the object will spin about an axis.

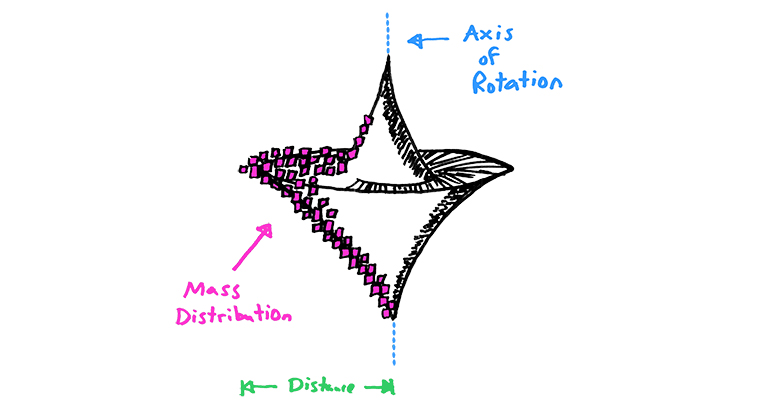
When swinging a golf club, you also need to apply a torque in order to whack the ball. Most of the golf club’s mass is located in the head. How does the mass distribution of the golf club affect torque?

How does the distance of an object’s mass from the axis of rotation affect the rotational speed of the object?

Golf isn’t the only sport where rotational inertia plays an important role. Take ice skating, for instance. Rotational inertia affects the athlete’s ability to perform different types of spins.

What happens when the ice skater changes the position of her arms?

What did you notice when the ice skater brought her arms closer to her body? What did you notice when she moved her arms away from her body? Her angular velocity changed, but why does it change so dramatically? The answer has to do with the relationship between her distribution of mass and her axis of rotation, and how it affects angular velocity. Let’s explore that relationship by creating a rotational inertia vehicle.

Materials (per vehicle)

Off to the races!

Using the rotational inertia vehicle and the Vehicle Data Sheet, you are going to test how fast the vehicle rolls down the ramp as the marbles are moved closer to the axis of rotation. (Note: You’re measuring the vehicle’s speed down the ramp as a proxy for angular velocity. The idea is that the faster the vehicle’s wheels rotate, the quicker the vehicle moves down the ramp.)

1. Measure the length, in millimeters, from the center of one marble to the center of the CD wheel converter. This number represents the distance from the distributed mass to the axis of rotation. (Because all the marbles are at the same distance from the center, you only need to measure the distance for one.)

   

2. Place the ramp at a 30-degree incline (use a protractor to find the angle). Set the vehicle at the top and release it. Measure the time it takes the vehicle to reach the bottom of the ramp, and record the time on the Vehicle Data Sheet.

   

3. Move the marbles 6 mm closer to the axis of rotation, and repeat steps 1 and 2.
4. Continue recording time and distance data until the marbles are at the axis of rotation.
5. Using the data collected, create a line graph of the mass’s distance from the axis of rotation versus time.

What did you notice when you graphed the data? Is there a pattern?

There is a direct relationship between mass distribution, its distance from the axis of rotation, and rotational inertia. How can you further modify the vehicle to make it faster? What do you think would happen if the marbles weren’t evenly spaced around the center?

Understanding rotational inertia can also help in analyzing the stability of objects that spin. Want to dig deeper into how rotational inertia affects stability? Check out this video from Disney Research.

As you observed in the previous activity, the distance of the vehicle’s mass from the axis of rotation affected the vehicle’s rotational inertia. Does this same relationship apply to eggs? Astronaut Don Pettit noticed that on Earth, hard-boiled eggs spin differently from raw eggs. He decided to investigate whether that difference occurs in zero gravity on the International Space Station.

Why do you think the liquid affects the egg’s rotation?

We may not be on the Space Station, but we can still test how eggs rotate on Earth. Try spinning a hardboiled egg and a raw egg on a table. What differences did you notice between the two eggs?

Challenge

Using clay and water-filled beads called Orbeez, you will simulate eggs that represent a range of stabilities and test their rotational inertia. What type of data should you collect to determine egg stability? Use the Egg Rotation Observation Sheet to record your data and observations. What structures in a raw egg and a hardboiled egg do the Orbeez and clay simulate?

Materials per group

• 6 clear plastic Easter eggs
• 1 stick of clay
• 1 pack of Orbeez balls
• 1 digital scale
• Stopwatch

Have a 3D printer? You can use this file (created by Joseph Equite, Lennox Math, Science and Technology Academy class of 2019) to create a special model of plastic eggs that you can fill with liquid for a more accurate experiment.

How does a liquid filling affect the rotation of an egg?

Testing Protocol

You will create six different eggs using the following protocol:

1. Fill one egg completely with clay, and record its mass using the digital scale. This will represent the control egg and the maximum mass for every other egg you create.
2. You will fill another egg, this time with some clay and some Orbeez. First measure the mass of the clay and the mass of the Orbeez, and record those numbers. Once you fill the egg, record its overall mass. Continue filling the rest of the eggs with different ratios of clay to Orbeez, remembering to record the mass for each type of filling, and the final mass of the egg.
3. Spin one egg on the table, point side-down, and record the time it takes the egg to fall on its side. Repeat for the remaining eggs, and try to use the same amount of force on the spin each time.

What did you notice as the amount of Orbeez increased inside the plastic eggs? How did increasing the amount of clay affect the egg’s rotation? Which egg do you think had the greatest rotational inertia? The least? Why do you think the Orbeez beads affect stability so much?

Once you’ve conducted your tests and are ready for an explainer, click here.

When designing new products, engineers must take into account how the item will react to different types of motion. This is especially important in sports, where a small edge in technology can mean a big difference in the performance of the athlete. How do you think engineers use rotational inertia to optimize golf clubs?

Learn more about the physics of the golf club with this video.

Vocabulary List

Torque – a perpendicular force acting at a distance from the axis of rotation that causes an object to rotate.

Angular Velocity – the rate at which an object’s rotational position changes with respect to time.

Next Generation Science Standards

Phenomenon Focus: The effect rotational inertia has on revolving systems.

Disciplinary Core Ideas and Performance Expectation

• PS2.A – Forces and Motion
• HS-PS2-1
• ETS1.B – Engineering Design
• HS-ETS1-2

Cross Cutting Concepts: Cause and Effect: Mechanism and Prediction, Systems and System Models, and Stability and Change

Scientific and Engineering Practice: Analyzing and Interpreting Data and Developing and Using Models

Common Core State Standards

RST.11-12.4: Determine the meaning of symbols, key terms, and other domain-specific words and phrases as they are used in a specific scientific or technical context relevant to grades 11-12 texts and topics.

WHST.9-12.7: Conduct short as well as more sustained research projects to answer a question (including a self-generated question) or solve a problem; narrow or broaden the inquiry when appropriate; synthesize multiple sources on the subject, demonstrating understanding of the subject under investigation.