Grade Level
3 - 5
minutes
1- 2 hrs
subject
Mathematics
Activity Type:
Bees, volume, surface area, perimeter, shapes
Honeybees have evolved over time to skillfully build hexagonal honeycomb cells. Why might a hexagon be a suitable shape for storing honey? Could other shapes, such as circles, triangles, or squares, work just as well?
Let’s investigate this question by first making some observations of a honeycomb. We’ll take a macro, or wide, perspective so we can study the honeycomb’s overall appearance. Then we’ll zoom in for a micro, or close-up, perspective in order to observe specific details.
From a macro perspective, what do you observe about the shape of honeycomb cells?

From afar, the cells might appear circular, as if they’re built to fit the elongated shape of a honeybee’s body.
Now let’s take a micro view and zero in on the cells.
From a micro perspective, what new details about the honeycomb cells did you observe?

Did you notice the hexagonal shape of the cells?
Scientists use their observations to make sense of the world we live in. When scientists come across a phenomenon and are puzzled by what they observe, such as the hexagonal shape of a honeycomb cell, they will often ask questions and try to understand the phenomenon by forming a “claim.”
You have made several observations of honeycomb cells. Let’s form a claim about the shape of those cells.
A scientific claim . . .
- answers a scientific question or problem and is usually a statement about, or understanding of, a phenomenon.
- is always supported by scientific data or “evidence.”
- provides “reasoning,” or a justification, that logically connects the evidence to the claim. It is usually based on a scientific definition, law, rule, or principle.
- can be revised as more evidence is gathered and/or logical connections are made that support changes in reasoning.
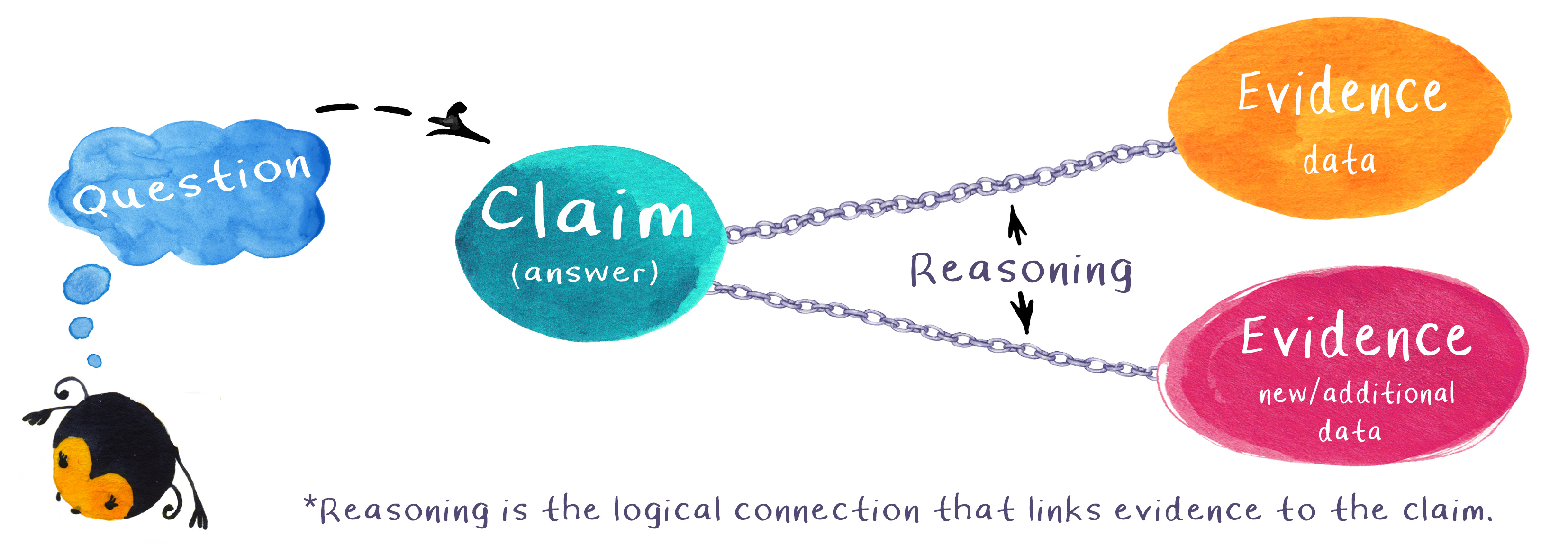
We often call the process of developing and explaining a claim “CER,” for Claim, Evidence, and Reasoning.
Why do honeybees use hexagonal shapes to construct their honeycombs?
Drawing from your observations of the honeycomb, use the CER worksheet to make a claim about why you think that the cells are shaped like hexagons.
See the Educator’s Toolbox for student worksheets and educator resources.
Honeycombs are made from beeswax, a substance created by worker bees. When the temperature is right, worker bees secrete wax scales from special glands in their body. Then they chew the wax with a bit of honey and pollen to produce the beeswax. The hexagonal cells serve as storage vessels for honey, as well as homes to raise young bees.

Bees must build their honeycomb efficiently.

Bees collect nectar and pollen from flowers to make honey, a sugary food, for the colony. Honey provides bees with the energy they need to survive and reproduce, as well as to build their homes. In order to make enough wax, worker bees need a lot of energy, and must therefore consume a lot of honey. Some studies estimate that bees must consume eight ounces of honey for every ounce of wax they produce. Imagine how many flowers a bee must visit to be able to convert nectar into eight ounces of honey!
On average, each bee can produce about 1/12 of a teaspoon of honey in its lifetime. If a bee were to provide one pound of honey, it would need to visit about 2 million flowers. A whole colony may travel about 55,000 miles in its lifetime!

Producing wax is hard work.
What would the proportion of honey consumed to wax produced look like? Measure water in a graduated cylinder (30 ml = 1 oz) to visualize the ratio.
- Measure out 8 oz of “honey” (water colored to look like honey).
- Measure out 1 oz of “wax” (regular water).
Compare the amount of honey and wax.

When building a honeycomb, bees must make sure they don’t waste more resources (wax) or expend more energy (honey) than necessary. This means that they need to use the least amount of wax possible to construct a comb that can store as much honey as possible.
Let’s investigate how different cell shapes might affect the amount of wax and space used to build a honeycomb.
You will conduct four investigations into how different types of shapes might affect the amount of wax and space needed to build cells in a honeycomb. Investigations should be conducted in sequential order, because each one builds upon previous investigations.
- Honeycomb Cell Shape Investigation
- Sharing Cell Walls Investigation
- Investigating Surface Area of Cell Shapes
- Investigating Volume of Cell Shapes
Honeycomb Cell Shape Investigation
Let’s imagine for a minute that we are worker bees. What would the honeycomb look like if the cells were different shapes? Using pennies and pattern blocks, or shapes cut from this template, you will experiment with different geometric shapes to see how well they would work as honeycomb cells. Try to arrange as many shapes together as possible with the least amount of wasted space. Remember, honeycomb cells are never a mixture of multiple shapes, so you can only use one shape at a time.
Thinking about the investigation:
- Based on your results, which shape appeared to be the worst shape for a honeycomb cell? Why?
- Shapes can be arranged to form other shapes. As you experimented with each type of shape, did you form any new ones?
Revisit the claim you wrote on your CER Worksheet. Is there new evidence that you could add to your CER? Are there any changes you would make to the claim based on your investigation?
Sharing Cell Walls Investigation
How can you collect mathematical evidence to support or revise your claim?

You may have noticed from the previous investigation that arranging circles resulted in big gaps between each shape. If honeycomb consisted of circles, there would be a lot of wasted space between cells, and a worker bee would probably have to expend a lot of energy filling in those gaps with wax.
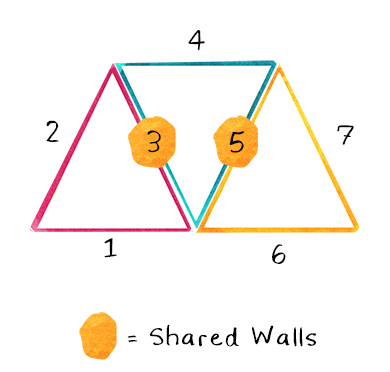
Other shapes can be more tightly arranged. There are three shapes you tested that can be organized so that no gaps appear between them: equilateral triangles, squares, and hexagons. The reason these shapes pack so well is because they have straight edges that line up against each other. In other words, these shapes can be positioned to share walls.
Let’s explore how well different shapes that share walls would work as honeycomb cells. Using different colored markers and the Sharing Cell Walls Worksheet, you will investigate which shape can be used to build a honeycomb with the greatest number of shared cell walls. Note that you’ll be covering an area with the same dimensions for each shape you investigate.
Materials
- Sharing Cell Walls Worksheet
- Various colored markers (or highlighters or colored pencils)
Do this activity in a group of three, so each person can work on one shape (triangle, square, hexagon)!
Thinking about the investigation:
Compare your data for each shape.
- Which shape required you to outline the most cell walls?
- Which shape required you to outline the fewest cell walls?
Did quantifying your data change or support your original claim about why bees might use hexagons to build their honeycomb cells? Add to (or revise) your original claim on your CER Worksheet.
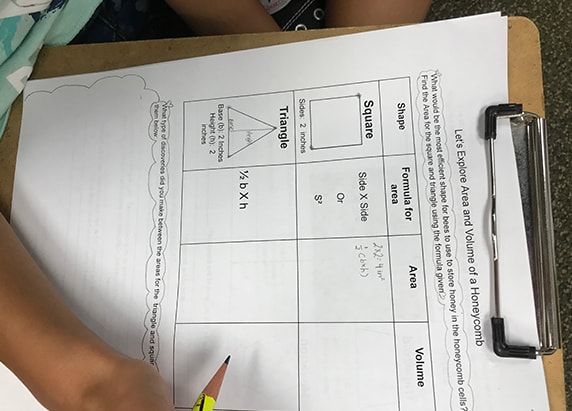
Investigating Surface Area Of Cell Shapes
By building honeycomb cells that share walls, bees can better conserve their resources (wax) and energy (honey). But don’t forget that bees use the combs as storage vessels for their honey. When bees construct their combs, they need to minimize the space between cells while maximizing the space available within the cell to store their honey.
Materials
● Exploring Surface Area and Volume of Cell Shapes Worksheet
● Working copy of CER Worksheet
Thinking about the investigation:
- Which shape had the greatest surface area?
- How could a honeycomb cell with a large surface area benefit a bee?
Revisit your CER Worksheet and continue to add to (or revise) your claim and/or evidence.
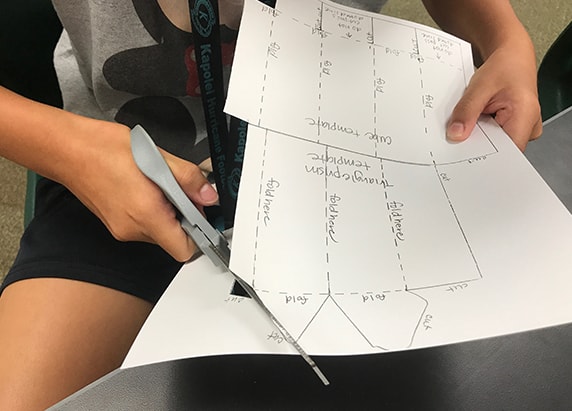
Investigating Volume Of Cell Shapes
From the area investigation above, you should have found that the hexagon had the greatest surface area of the shapes you tested. Now let’s explore the volume of different shapes. We will use cell-shaped prisms to help us with this investigation.
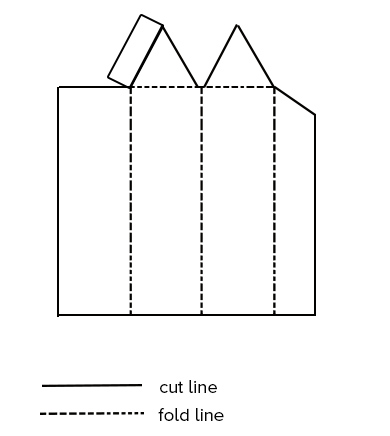
Materials
- Prism Template
- Exploring Surface Area and Volume of a Honeycomb Cell Worksheet
- Scissors
- Tape
- Sand
- Funnel or old coffee cups with travel lid for pouring sand
- Graduated cylinder
Thinking about the investigation:
Compare the volume of all your shapes. Which shape would store the most amount of honey?
Revisit your CER Worksheet and continue to add to (or revise) your claim and/or evidence.
Assessment — Revisiting And Revising Your Claim Statement
Revisit the original question at the beginning of this lesson:
Why do honeybees use hexagonal shapes to construct their honeycombs?
Reflect on your findings from the four investigations.
- Which shape was associated with the fewest spaces between shapes?
- Which shape was associated with the most shared walls?
- Which shape had the greatest surface area?
- Which shape had the greatest volume?
Use the Claim-Evidence-Reasoning (C-E-R) method to revise or add to the claim on your worksheet. Be sure to include data based on your findings from the four different investigations.
- In the Honeycomb Cell Shape Investigation, what evidence did you gather that helped you revise or support your claim?
- What evidence did you gather from the Sharing Cell Walls Investigation that helped you revise or support your claim?
- What evidence did you gather from the Investigating Surface Area of Shapes activity that helped you revise or support your claim?
- What evidence from the Investigating Volume of Shapes exercise helped you revise or support your claim?
The Honeycomb Conjecture
In ancient times, a Roman scholar named Marcus Terentius Varro studied his collection of bees and proposed that the hexagonal structures that honeybees build are more compact than any other shape. But it was thousands of years later—in 1999, in fact—that a mathematician at the University of Michigan named Thomas Hales was able to provide mathematical proof of what is known as the “Honeycomb Conjecture.” Hales concluded that the more compact the shape of the honeycomb cell was, the less energy and wax a bee would use to build it, which meant that bees could expend their energy on other important activities—specifically, foraging and making honey.
Learn more about how Thomas Hale solved the hexagonal honeycomb mystery in this short BBC video.
Extensions
Would you like to experience what it’s like inside a beehive? Take a look at the Science Friday article Step Into a Hive, by Chau Tu, to see how sculptor Wolfgang Buttress created the experience of being inside a beehive.

- After reading “Step Into a Hive,” explore how bees are able to communicate.
- Explore bubbles as they connect to form hexagons.
Additional Video Resources
Next Generation Science Standards
- Disciplinary Core Idea: LS1. A Structure and Function
- Crosscutting Concepts: Structure and Function, Patterns, Cause and Effect
Common Core State Standards: Standards of Mathematical Practice
- SMP 3: Construct viable arguments and critique the reasoning of others
- SMP 4: Model with mathematics
- SMP 7: Look for and make use of structure
- SMP 8: Look for and express regularity in repeated reasoning
Teachers who field tested this resource had the following advice for teachers adopting this resource:
Betsy from Kansas said:I loved how the students were able to use the evidence from each of the investigations to support the claim as to why honeybees use the hexagon. I also loved the questions that students were having based on the investigations. I had one student ask if wasps were similar to the honeybee in how they love and create their homes.
Rose from Georgia said: I supplemented “activators” by having some bee trivia facts to each opening session. Incentives included “busy as a bee” badges and small treats to keep the hive Bzzzzy! The best part was the hands-on activities that allowed true connection to the content. The conclusions were easy to determine at the student level with the completed activity sheets.
Educator's Toolbox
Meet the Writer
About Stacy George
Stacy George is a STEM teacher for grades three through five at Mauka Lani Elementary School in Hawaii. After more than 25 years of teaching, she’s convinced that getting messy is key to learning about science, so it’s no surprise to see her out with her students digging for worms or testing the water quality of local streams.